회귀 분석
회귀 분석이란 데이터를 가장 잘 설명하는 모델을 찾아 입력값에 따른 미래 결과값을 예측하는 알고리즘이다.
완벽한 예측을 불가능하기에 최대한 잘 근사해야 한다. 각 데이터의 실제 값과 모델이 예측하는 값의 차이를 최소한으로 하는 선을 찾아야 한다.
단순 선형 회귀
데이터를 설명하는 모델을 직선 형태로 가정한다. 데이터를 가장 잘 설명하는 β를 찾는 것.

데이터를 잘 설명한다는 것은, 실제 정답과 내가 예측한 값과의 차이가 작을 때이다.

단순 (실체값 - 예측값)은 부호 때문에 합계를 내면 이 차이를 정확히 나타내지 못한다. 부호가 상쇄하는 것을 막기 위해 (실제값 - 예측값)의 제곱을 통해 판단한다.
Loss 함수
실제 값과 예측 값 차이의 제곱의 합을 Loss 함수로 정의한다. 따라서 Loss 함수가 작을 수록 좋은 모델이다.

입력값을 X, 예측값을 y ̅, 실제값을 y(i)라고 한다.
Loss 함수에서 주어진 값은 입력 값과 실제 값이라서, β0와 β1 값을 조절하여 Loss 함수의 크기를 줄여야한다.
최적의 베타를 찾는 방법에는 대표적으로 경사 하강법(Gradient descent)이 있다.
경사 하강법
1) 랜덤 초기화 : 베타 제로와 베타 원 값을 초기화한다.
2) Loss 값 계산
3) Gradient 계산 : Gradient은 미분 값, 경사도이다.
4) β0, β1 업데이트 : 경사도가 낮은 쪽으로 업데이트한다.

단순 선형 회귀는 1) 데이터 전처리 후 2) 단순 선형 회귀 모델 학습 (경사 하강법)을 진행하고 3) 새로운 데이터에 대한 예측을 하는 과정으로 나타낼 수 있다. 가장 기초적이나 여전히 많이 사용되는 알고리즘이지만, 입력값이 1개인 경우에만 적용이 가능하다. 입력값과 결과값의 관계를 알아보는데 용이하다. 입력값이 결과값에 얼마나 영향을 미치는지 알 수 있고, 두 변수 간의 관계를 직관적으로 해석하고자 하는 경우에 활용한다. 기울기의 부호나 크기에 따라 X와 Y의 관계가 여러 의미로 해석할 수 있기 때문이다.
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]
# 모델을 전 처리합니다.
train_X = pd.DataFrame(X, columns=['X'])
train_Y = pd.Series(Y)
# 모델을 트레이닝합니다.
lrmodel = LinearRegression() # 모델 초기화
lrmodel.fit(train_X, train_Y) # 모델 학습
# train_X에 대해서 예측합니다.
pred_X = lrmodel.predict(train_X) # predict() 를 이용하여 예측
print('train_X에 대한 예측값 : \n{}\n'.format(pred_X))
print('실제값 : \n{}'.format(train_Y))
다중 선형 회귀
여러 개의 입력값으로 결괏값을 예측하고자 하는 경우, 다중 선형 회귀(Multiple Linear Regression)을 이용한다.
입력값 X가 여러 개(2개 이상)인 경우 활용할 수 있는 회귀 알고리즘으로, 각 개별 X에 해당하는 최적의 β를 찾아야 한다.

단순 선형 회귀와 마찬가지로 Loss 함수는 입력값과 실제값의 차이의 제곱의 합으로 정의한다.

마찬가지로 β값을 조절하여 Loss 함수의 크기를 작게 한다.
여러 개의 입력값과 결과값 간의 관계를 확인 가능하다. 어떤 입력값이 결과값에 어떠한 영향을 미치는지 알 수 있다. 여러 개의 입력값 사이 간의 상관 관계*가 높을 경우 결과에 대한 신뢰성을 잃을 가능성이 있다. X끼리 독립 변수가 아니라 관계가 있는 값(*상관 관계 : 한 쪽이 변하면 다른 한 쪽도 변하는 것)이 있으면 해당 X는 과감하게 버리는 것이 좋다.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 데이터를 읽고 전 처리합니다
df = pd.read_csv("data/Advertising.csv")
df = df.drop(columns=['Unnamed: 0'])
# 1. Sales 변수는 label 데이터로 Y에 저장하고 나머진 X에 저장한다.
X = df.drop(columns=['Sales'])
Y = df['Sales']
# 2. 2:8 비율로 (test_size = 0.2) X와 Y를 학습용과 평가용 데이터로 분리한다.
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
# 3. 다중 선형 회귀 모델을 초기화 하고 학습합니다
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
print('test_X : ')
print(test_X)
# 4. test_X에 대해서 예측합니다.
pred_X = lrmodel.predict(test_X) # predict()를 활용해서 예측합니다.
print('test_X에 대한 예측값 : \n{}\n'.format(pred_X))
# 5. 새로운 데이터 df1을 정의합니다
df1 = pd.DataFrame(np.array([[0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 1, 1]]), columns=['FB', 'TV', 'Newspaper'])
print('df1 : ')
print(df1)
# 6. df1에 대해서 예측합니다.
pred_df1 = lrmodel.predict(df1) # predict()를 활용해서 예측합니다.
print('df1에 대한 예측값 : \n{}'.format(pred_df1))
회귀 평가 지표
목표를 얼마나 잘 달성했는지 정도를 평가해야한다. 실제 값과 모델이 예측하는 값의 차이에 기반한 평가 방법을 사용하는데, 대표적으로 RSS, MSE, MAE, MAPE, R2 등이 있다.
RSS - 단순 오차
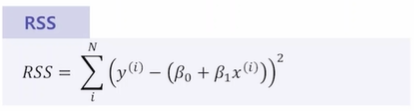
실제 값과 예측 값의 단순 오차 제곱의 합이다. 값이 작을수록 모델의 성능이 높다.가장 간단한 평가 방법으로 직관적인 해석이 가능하나 오차를 그대로 이용하기 때문에 입력 값의 크기에 의존적이다. 절대적인 값과 비교가 불가능하다. 데이터가 10개일 때랑 100개일 때랑 비교가 불가능한 것이다.
MSE (Mean Squared Error)

평균 제곱 오차, RSS에서 데이터 수만큼 나눈 값이다. 작을수록 모델의 성능이 높다고 할 수 있다.
이상치와 같은 데이터들 중 크게 떨어진 값에 민감하다.
MAE (Mean Absolute Error)

평균 절대값 오차, 실제 값과 예측 값과 오차의 절대값의 평균이다. 작을수록 모델의 성능이 높다고 할 수 있다.
변동성이 큰 지표와 낮은 지표를 같이 예측할 시 유용하다.
가장 간단한 평가 방법들로 직관적인 해석이 가능하다. 그러나 평균을 그대로 사용하기 때문에 입력 값의 크기에 의존적이다. 절대적인 값과 비교가 불가능하기도 하다. 모델 A는 키에 대해 예측하고 모델 B는 몸무게에 대해 예측한다고 하자. 일반적으로 키가 몸무게보다 Scale이 크다. 그래서 MSE나 MAE도 모델 A가 클 확률이 높다. 모델 A와 B의 성능을 비교할려고 할 때 MSE와 MAE를 통해 비교하고자 하는 건 한게가 있다.
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
# 다른 모듈도 불러왔다 가정하고 데이터 전 처리, 학습, 예측도 마쳤다고 하자.
"""
1. train_X 의 MSE, MAE 값을 계산합니다
"""
MSE_train = mean_squared_error(train_Y, pred_train) # mean_squared_error() 를 활용해서 MSE를 계산합니다.
MAE_train = mean_absolute_error(train_Y, pred_train) # mean_absolute_error() 를 활용해서 MAE를 계산합니다.
print('MSE_train : %f' % MSE_train)
print('MAE_train : %f' % MAE_train)
# test_X 의 예측값을 계산합니다
pred_test = lrmodel.predict(test_X)
"""
2. test_X 의 MSE, MAE 값을 계산합니다
"""
MSE_test = mean_squared_error(test_Y, pred_test) # mean_squared_error() 를 활용해서 MSE를 계산합니다.
MAE_test = mean_absolute_error(test_Y, pred_test) # mean_absolute_error() 를 활용해서 MAE를 계산합니다.
print('MSE_test : %f' % MSE_test)
print('MAE_test : %f' % MAE_test)R2 (결정 계수)
회귀 평가 지표 중 하나. 회귀 모델의 설명력을 표현하는 지표로, 1에 가까울수록 높은 성능의 모델이라 해석할 수 있다. 작아질수록 안 좋은 성능을 보이는 모델이다.

여기서 TSS는 데이터의 평균 값과 실제 값(y(i))차이의 제곱이다.

오차가 없을수록 1에 가까운 값을 얻는다. 값이 0인 경우, 데이터의 평균 값을 출력하는 직선 모델을 의미한다. 음수 값이 나온 경우, 평균 값 예측보다 성능이 좋지 않은 경우를 의미한다. 그니까 R2<0는 마치 시험에서 찍었는데 다 틀린 경우… 라고 볼 수 있다.

# 다른 모듈도 불러왔다 가정하고 데이터 전 처리, 학습, 예측도 마쳤다고 하자.
from sklearn.metrics import r2_score
"""
1. train_X 의 R2 값을 계산합니다
"""
R2_train = r2_score(train_Y, pred_train) # r2_score()를 활용하여 R2값을 계산합니다.
print('R2_train : %f' % R2_train)
# test_X 의 예측값을 계산합니다
pred_test = lrmodel.predict(test_X)
"""
2. test_X 의 R2 값을 계산합니다
"""
R2_test = r2_score(test_Y, pred_test) # r2_score()를 활용하여 R2값을 계산합니다.
print('R2_test : %f' % R2_test)'AI / DL > 엘리스 AI 데이터 분석 트랙' 카테고리의 다른 글
| [AI 데이터 분석] 딥러닝 시작하기 01. 퍼셉트론 (0) | 2022.10.08 |
|---|---|
| [AI 데이터 분석] 머신러닝 시작하기 04. 지도학습 - 분류 (0) | 2022.10.07 |
| [AI 데이터 분석] 머신러닝 시작하기 02. 데이터 전 처리하기 (0) | 2022.10.07 |
| [AI 데이터 분석] 머신러닝 시작하기 01. 자료 형태의 이해 (0) | 2022.10.06 |
| [AI 데이터 분석] 머신러닝 시작하기 00. 인공지능/머신러닝 개론 (0) | 2022.10.06 |




댓글